INSTRUÇÃO DE SERVIÇO Nº 002/91-DFIS, DE 30 DE ABRIL DE 1991

Dispõe sobre o controle de produtos agrícolas depositados.

O DIRETOR DO DEPARTAMENTO DE FISCALIZAÇÃO da Superintendência da Receita Estadual, no uso de suas atribuições e

CONSIDERANDO que a atuação da Administração Tributária, no que se refere ao programa "Produtos Agrícolas", envolve dois momentos específicos, quais sejam o controle dos produtos depositados e a fiscalização verticalizada do contribuinte;

CONSIDERANDO a impossibilidade ou inoportunidade, dadas a exiguidade de tempo de carência de recursos humanos, de se implementar, simultaneamente, as duas etapas de trabalho;

CONSIDERANDO que o trabalho de controle dever ser desenvolvido em caráter de urgência, vez que esta etapa é fundamental, não somente como elemento de impacto, mas também como procedimento inicial da rotina de fiscalização a ser implementada "a posteriori";

CONSIDERANDO a necessidade de uniformizar os procedimentos de controle de produtos agrícolas depositados em Armazéns de Terceiros, Armazéns Gerais, Depósitos Fechados, Cooperativas de Produtores e Empresas Cerealistas, e

CONSIDERANDO, finalmente, que o controle dos produtos depositadas nos estabelecimentos acima, será executado pelas Delegacias da Recita Estadual, com a utilização de agentes do Fisco previamente designados e orientados,

ESTABELECE:

1 - QUANTO À ANÁLISE CADASTRAL

Com relação a este item, o agente do Fisco deverá adotar as seguintes providências:

1.1 - Verificar se o contribuinte encontra-se regularmente cadastrado no CCE/GO, mediante a apresentação da FIC ou FAC, conferido nome, endereço, endereço e ramo de atividade, entre outros dados;

1.2 - Conferir se os atuais proprietários do estabelecimento são aqueles constantes do Contrato Social ou Declaração para Registro de Firma Individual;

1.3 - Proceder as devidas intimações no sentido de sanar as irregularidades detectadas.

2 - QUANTO AO TRANCAMENTO DOS BLOCOS DE DOCUMENTOS FISCAIS:

Relativamente a esta fase do trabalho, o funcionário deverá:

2.1 - Solicitar do responsável pelo estabelecimento a apresentação dos blocos de Notas Fiscais, de todas as séries e subséries, e da Requisição de documentos Fiscais (RD-8) em uso;

2.2 - Lavrar, no verso dos últimos documentos fiscais emitidos (NF e RD-8), termo de trancamento consignado, além da observação com o seguinte teor: "Última Nota Fiscal (ou RD-8) emitida - estabelecimento sob Ação Fiscal", a data, assinatura, cargo e cadastro funcional da autoridade fiscal;

2.3 - Tomar o cuidado de cancelar os documentos fiscais que por ventura não tenham sido utilizados na seqüência correta, conforme previsto no artigo 8º, §§ 2º e 3º do Decreto nº 969/79; e

2.4 - Relacionar, no espaço próprio do formulário de trancamento de estoque as últimas Notas Fiscais, por série e subsérie, e RD-8 emitidas, objeto do procedimento inserido no item 2.2.

3 - QUANTO AO TRANCAMENTO DO ESTOQUE EXISTENTE:

No que concerne a este item, o agente do Fisco adotará os seguintes procedimentos:

3.1 - Realizar a contagem física do estoque existente de produtos agrícolas, com acompanhamento do proprietário ou responsável pelo estabelecimento, com vistas a evitar qualquer dúvida ou desacerto (colhendo, ao final, a sua assinatura), de acordo com o roteiro contido no Anexo Único;

3.2 - Relacionar os produtos por espécie, separando, inclusive, os em estado natural dos beneficiados, observada a respectiva unidade de medida;

3.3 - Verificar a existência de estoque de sacaria nova ou usada, material de embalagem, sacos plásticos personalizados e outros;

3.4 - Providenciar para que uma via do formulário de trancamento de estoque, devidamente preenchida (observadas as recomendações do roteiro anexo) e assinada, seja encaminhada à Delegacia da Receita Estadual, para efeito de arquivamento em pasta (dossiê) individual do contribuinte;

3.5 - Exigir do estabelecimento depositário a apresentação das plantas que serviram de base à edificação, de onde serão extraídos os dados necessários à contagem do estoque, na forma e condições constantes do roteiro anexo.

4 - QUANTO À RESPONSABILIDADE DA DELEGACIA DA RECEITA ESTADUAL;

O seu titular deverá:

4.1 - Adotar as medidas necessárias a manter atualizado o arquivo mencionado no item 3.4. para que, no momento em que for desencadeada a fiscalização verticalizada sobre o contribuinte, o agente do Fisco possa sempre tomar por base o(s) trancamento(s) de estoque realizado(s);

4.2 - Fornecer aos funcionários designados para a tarefa prevista nesta instrução, o material necessário, com vistas ao aperfeiçoamento dos resultados;

4.3 - Zelar pela regularidade dos referidos trancamentos, esforçando-se por realizá-los ao menos uma vez ao mês, em cada contribuinte.

GABINETE DO DIRETOR DO DEPARTAMENTO DE FISCALIZAÇÃO da Superintendência da Receita Estadual, em Goiânia, 30 de abril de 1991.

Miguel Avelar Filho

DIRETOR

ANEXO ÚNICO À INSTRUÇÃO DE SERVIÇO Nº 002/91

TRANCAMENTO FÍSICO DE ESTOQUES DE CEREAIS

O trancamento de estoques de cereais, na forma em que geralmente é realizado, tem-se revelado um instrumento inócuo para a fiscalização, seja por superestimar o volume real encontrado (não logrando a concordância do depositário), seja por aceitar a "verdade" inscritas nas fichas de controle apresentadas pelos estabelecimentos, nem sempre confiáveis.

Preocupados com essa situação, deliberamos buscar informações que nos pudessem auxiliar a desenvolver uma contagem justa, o mais aproximada possível da realidade. Além de investigarmos toda uma literatura especializada, obtivemos a colaboração de diverso órgãos ligados à armazenagem, especialmente da Companhia Nacional de Abastecimento - CNA, de cuja equipe técnica recebemos os dados que basicamente possibilitaram a elaboração do presente roteiro.

Lançando mão de ferramentas científicas, o fiscal não precisará mais se submeter às cansativas "argumentações" de alguns armazenadores, sempre tendentes a subavaliar o volume de grãos colocadas sob sua responsabilidade.

Vale dizer que a obviedade dos resultados apurados pelos métodos aqui apresentados é inquestionável, pois eles se fundamentam estritamente em cálculos matemáticos e no conteúdo de pesquisas estatísticas. Contudo, deverá o funcionário usar de toda a sua criatividade ao transportar para o papel tudo o que ele realmente enxergar, visando evitar que a frieza das fórmulas possa mais uma vez nos afastar do que de fato existe.

I - CÁLCULO DA CAPACIDADE ESTÁTICA:

Imaginemos, em primeiro lugar, que o estabelecimento objeto de nossa verificação, esteja lotado e obedeça aos padrões de armazenagem estabelecidos pelo Ministério da Agricultura. Isso facilitará sobremaneira o nosso trabalho, pois apenas precisaremos calcular a quantidade máxima de grãos que suportaria o armazém (a sua capacidade estática).

I.1 - CAPACIDADE ESTÁTICA DOS ARMAZÉNS CONVENCIONAIS:

Para alcançá-la, podemos nos utilizar da seguinte fórmula:

C = 0,55 x V x n

Sendo:

C = capacidade estática do armazém

0,55 = coeficiente (indicativo do volume útil ocupado) dado

V = volume total do armazém (comprimento x largura x pé-direito ou altura)

n = nº de sacos/m³ (conforme tabela auxiliar de nº 01)

Entretanto, a fórmula anterior só terá eficácia se obedecidas as seguintes condições:

a) afastamento lateral (parede-pilha = 0,80m);

b) largura do arruamento principal ou rua longitudinal = 2,40m;

c) largura do arruamento secundário ou rua transversal = 1,20m;

d) altura da pilha (armazém c/6,0m de pé-direito) = 4,50m;

e) considerando sacarias padronizadas de acordo com normas da CNA (Cia Nacional de Abastecimento) sucedânea da CFP.

I.2 -CAPACIDADE ESTÁTICA DAS UNIDADES GRANELEIRAS:

Devido à grande variedade de configuração das unidades graneleiras, tornam-se um pouco mais complicados os cálculos, pelo que precisaremos de algumas outras informações básicas.

De qualquer forma, através das plantas (baixas, de cortes, de situações etc) exigidas das edificações depositárias, obteremos com facilidade as figuras geométricas que compõem a conformação total da unidade.

TABELA 01

PRODUTO	NÚMERO DE SACAS POR m^3	TONELADAS/m^3 (GO) (saca 60 Kg)
Arroz em casca	09	0,57
Café beneficiado	10	0,60
Farinha de Trigo	10	0,60
Farinha de Mandioca	10	0,60
Arroz descascado	11	0,66
Feijão	11	0,66
Milho (em Grão)	11	0,75
Trigo (em Grão)	11	0,66
Soja	11	0,66
Açúcar	12	0,72

Fonte: Manual do Armazenista, Filadelfo Brandão, p.66

Depois disso, basta-nos aplicar as fórmulas, indicadas a seguir.

I.2.1 - Capacidade Estática dos Silos:

Para, se chegar à capacidade total do silo, deve-se buscar a de cada célula em primeiro lugar:

C = 0,94 x V x (P.E)

Sendo:

C = capacidade estática, em toneladas (t)

0,94 = coeficiente dado (correspondente a volume útil de ocupação da célula)

V = Volume total da célula, em m³

P.E. = peso específico do grão, em t/m³ (vide tabela 2)

Pelo que se apresenta, portanto, a dificuldade consiste em se conhecer o volume total da célula, que normalmente assume a seguinte configuração:

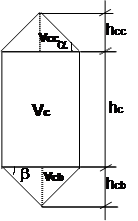
Sendo:

H_CC = altura do cone da cobertura

h_c = altura do cilindro

h_cb = altura do cone da base

= ângulo do cone da cobertura, de repouso

(convencionado em 30º)

= ângulo do cone da base, ou de descarga

(convencionado em 45º)

V_cc = volume do cone da cobertura

V_c = volume do cilindro

V_cb = volume do cone da base

V_t = volume total da célula = V_cc+V_c+V_cb

Para descobrirmos o V_t, portanto, deveremos calcular o volume de cada uma das figuras que compõem a célula.

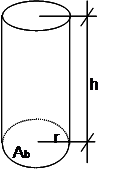Assim:

1º passo: cálculo do volume do cilindro;

Sendo:

V_c = volume do cilindro

A_b = área da base = (círculo)

h_c = altura do cilindro (obtida diretamente)

r = raio da base

= constante = 3,1416

2º passo: cálculo do volume do cone da base (de descarga)

V_cb = x A x h_cb

Sendo:

V_cb = volume do cone da base

A = r²(área do círculo)

h_cb = altura do cone da base(h_cb = tg x r)

Sendo b = 45º e sabendo-se que a tangente de 45ºé igual a 1, temos:

h_cb = 1 x r

Note-se, que, no nosso caso, a área do círculo do cone é a mesma da base do cilindro.

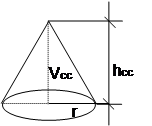3º passo: volume do cone da cobertura:

V_cc = x A x h_cc

Sendo:

A = círculo da base ( )

h_cc = altura do cone da cobertura (h_cc = tg x r).

Sendo = 30º e sabendo-se que a tangente de 30º é igual a 0,58, temos: h_cc = 0,58 x r

Uma vez obtida a capacidade de cada célula, teremos a capacidade estática do silo resulta do somatório de todas elas;

I.2.2 - Capacidade estática dos ARMAZÉNS GRANELEIROS (sem septo divisório):

C = 0,72 x V x (PE)

onde:

C = capacidade estática em toneladas (t)

0,72 = coeficiente dado (relativo ao volume útil)

V = volume total interno do armazém, em m³

P.E. = peso específico, em t/m³ (vide tabela 02)

Do mesmo modo que no item anterior, a solução do problema está em se identificar as formas geométricas componentes da estrutura. O mesmo procedimento deverá ser adotado quando o graneleiro possuir dois ou mais compartimento ( com septo) sendo que nesse caso o coeficiente dado, relativo ao volume útil, é de 0,64.

Complementando, aconselhamos a elaboração de um croqui para cada figura idealizada, com a indicação das medidas utilizadas, que deverá acompanhar o termo de trancamento, principalmente se o mesmo redundar em lançamento de crédito tributário.

TABELA 02

PESO ESPECÍFICO DE GRÃOS E MATERIAIS PULVERULENTOS DESTINADOS À ALIMENTAÇÃO

PRODUTO	TONELADA/m^3
	MÍNIMO	MÉDIO	MÁXIMO
Amendoim descascado	0,34	0,38	0,42
Arroz beneficiado	0,75	0,78	0,82
Arroz em casca	0,58	0,60	0,62
Aveia	0,43	0,48	0,54
Café beneficiado	0,54	0,60	0,68
Café coco(c/casca)	0,34	0,38	0,42
Centeio	-	0,70	-
Cevada	0,55	0,63	0,69
Farinha de mandioca	-	0,51	-
Farinha milho(fubá)	-	0,88	-
Farinha de trigo	0,50	0,59	0,67
Feijão	0,75	0,78	0,81
Leite em pó	-	0,60	-
Milho em Grão	0,72	0,75	0,82
Sementes de algodão	-	0,42	-
Soja em grão	0,75	0,80	0,84
Sorgo	0,67	0,71	0,75
Trigo em grão	0,75	0,79	0,84

Fonte "Armazéns e Silos - Preservação de Grãos Alimentícios", Dasp, 1964.

II - LEVANTAMENTO DO ESTOQUE FÍSICO EXISTENTE:

Analisamos anteriormente situações em que as unidades armazenadoras encontravam-se completamente cheias, o que nos facilita sobremaneira o trabalho, pois as medidas necessárias para o cálculo do volume são encontradas diretamente nas plantas fornecidas

Entretanto, na maioria das vezes nos depararemos com graneleiros semivazios ou mesmo armazéns totalmente indisciplinados quanto às normas baixadas pela CNA. Nesse momento, então, fará diferença a maior ou menor diligência e capacidade de improvisação do colega, já que teremos de coletar as medidas por nossa própria iniciativa, através de verificação local, inclusive por sobre pilhas ou amontoados de grãos (nesse caso, será indispensável de uso de uma trena, que deverá ser fornecida pela Delegacia da Receita Estadual).

II.1 - Estoque Físico dos Armazéns convencionais

(carga parcial)

Quando este tipo de depósito não obedecer aos parâmetros exigidos, ou mesmo se não estiver com a sua capacidade total esgotada, a contagem deverá ser implementada pilha a pilha, medindo-se a sua largura (I), a sua altura (h) e o seu comprimento (c) para posterior aplicação da seguinte operação:

V_pilha = l x h x c

Uma vez encontrado o volume da pilha, basta-nos procurar na tabela 01 a quantidade de sacas que cabem em cada metro cúbico do produto em questão, chegando ao total através de uma regra de três simples.

II.2 - Estoque Físico das Unidades Graneleiras

(carga parcial)

E_f = V_e x (PE)

Sendo:

E _f = Estoque físico

V _e = volume efetivo (existente)

PE = peso específico (tabela 02)

Você deverá notar que nesse caso não será utilizado nenhum daqueles coeficientes de volume útil ocupado. Sendo na prática um "desconto" aplicado no cálculo da capacidade estática, concebido em função dos espaços necessariamente ociosos, variáveis em cada espécie de unidade armazenadora, tais coeficiente são plenamente dispensáveis a partir deste momento, já que a nossa medição reportar-se-á exclusivamente aos montes encontrados.

Com efeito, a única dificuldade agora, em que pese seja relativa, é a obtenção do volume efetivo, pois o acesso aos amontoados de cereais nem sempre é possível. A nossa alternativa seria, especialmente no caso das células dos silos, optar pelo método dedutivo: fixando-se um peso na ponta da trena e arremessando-a para dentro da célula, obteremos com facilidade os graus do maior e do menor espaços vazios; em seguida, subtraindo-os da altura fornecida pela planta baixa, encontraremos os dois dados que nos faltavam para a resolução do problema, quais sejam a altura do cilindro (h_c) e a altura do cone de cobertura, ou de repouso (h_cc).

Dissemos que apenas estes dois dados nos faltavam porque os demais, ou são convencionais, como o ângulo de repouso (=30º) e o de descarga (b = 45º), ou são detectados através da simples averiguação da planta (diâmetro do cilindro, por exemplo).

No caso dos armazéns graneleiros, pode-se inclusive andar por sobre os montes, livremente ou com a ajuda de tábuas, se houver dúvida quanto à sua consistência. Na verdade, quanto mais próximo do objeto de observação estiver o colega, melhor condição ele terá de manter-se fiel à configuração encontrada, reduzindo assim a margem de erro do cálculo final.

Finalizando, recomendamos que sejam tentadas, na medida do possível, adaptações que facilitem o nosso trabalho, como ajuntamento de grãos dispersos e paralisação temporária da circulação dos produtos, vez que a precisão na contagem interessa também ao contribuinte.

ALGUMAS FÓRMULAS PARA CÁLCULO DE ÁREA E VOLUME:

NOMENCLATURA:

a,b,c e d - comprimento dos lados h_g - distância vertical entre os centros da gravidade das áreas

C - comprimento de corda L - comprimento lateral

A - área total P - perímetro

A_b - área da base P_b - perímetro da base

A_L - área de superfícies convexas P_t - perímetro do topo da seção

A_r - área da seção direita V - volume

A_t - área do topo da seção d,d₁,d₂ - diâmetro

h,h₁,h₂ - altura c,f - comprimento das diagonais

r,r₁,r₂,R - raio n - número de lados

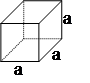
1. CUBO A = 6a²

V = a³

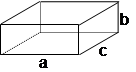
2. PARALELOGRAMO A = 2(ab+bc+ac )

V = abc

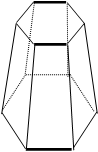
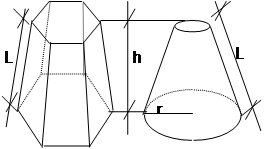
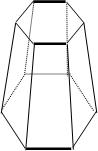
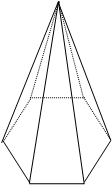
3. PIRÂMIDE OU CONE A_L =L(p_b+p_t )

A = A_L +A_b +A_t

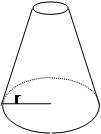V =

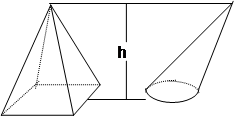
4. PIRÂMIDE REGULAR

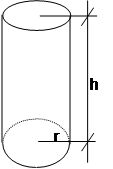
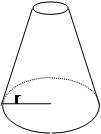CERTA OU CONE V = A_bh

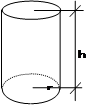
5. CILINDRO NORMAL A_L= 2rh

A = 2r(r+h )

V = r² h

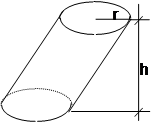6. CILINDRO INCLINADO A_L = p_b h = p_b L

A = A_L+2A_b

V = A_b h=A_b L

7. ESFERA A = 4r² = 12,566 r²

V =r³ = 4,189 r³

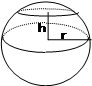
8. SETOR DA ESFERA V = r² h = 2,0944 r² h

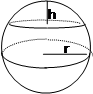
9. SEGMENTO DA ESFERA

V = h ²(3r - h)

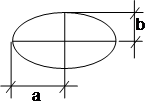
10. ELIPSE A = ab

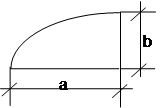
11. PARÁBOLA

A = ab

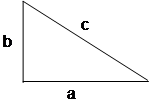12.TRIÂNGULO RETÂNGULO

P = a+b+c

c²=a²+b²

b =

A =

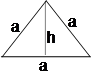13. TRIÂNGULO EQUILÁTERO

P = 3a

h =

A =

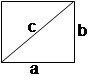14. QUADRADO a = b

P = 4a

A = a²

c = a

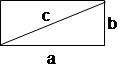15. RETÂNGULO P = 2(a+b)

c =

A = ab

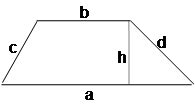
16. TRAPÉZIO P = a+b+c+d

17. POLÍGONO REGULAR Seja n = número de lados

P = n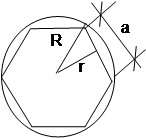a

A =

18. CÍRCULO P = 2r

A = r²